
对于平均数问题、浓度问题、利润问题、增长率问题、比重问题等混合问题,一般可以采用十字交叉来实现多的量和少的量保持平衡。这也是十字交叉法的核心。实际上十字交叉法是进行混合物平均量计算的一种简便方法。
十字交叉法的具体形式比较简单,包括五部分:部分平均量、总体平均量、交叉作差、对应比、对应实际量。掌握三组计算关系、四种题型。具体模型如下:
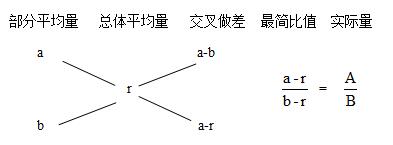
三组计算关系:
第一组:第一列和第2列交叉作差等于第三列;
第二组:第3/4/5列比值相等;
第三组:第1列的差等于第3列的和。
四种题型:
1) 已知总体平均量、第一部分平均量、对应之比,求第二部分平均量
2) 已知总体平均量、第二部分平均量、对应之比,求第一部分平均量
3) 已知第一部分平均量、第二部分平均量、对应之比,求总体平均量
4) 已知第一部分平均量、第二部分平均量、总体平均量,求对应之比
接下来用几道常见示例来讲解具体如何来用十字交叉法速算:
例1:一批商品按期望获得50%的利润来定价,结果只卖掉了70%的商品,为了销售掉商品,商店决定按定价打折出售,这样获得的利润是原来的82%,打了多少折?
A 4折 B 6折 C 7折 D 8折
【解析】题干设计到平均量混合问题,可以尝试运用十字交叉法求解。所求为折扣,根据折扣公式需知道两个部分平均量的值。建立模型,标识出五部分内容,已知部分平均量的值a为50%,总体平均量r=50%×82%=41%,以及两个实际量的值分别是70%、30%。

例2:小王登山,上山的速度是每小时4km,到达山顶后返回,速度为每小时6km,设山路长为9km,小王的平均速度为( )km/h。
A .4.8 B .5 C .4.4 D .4.6
【解析】简单行程问题,可以利用图解法或者正反比例求解。但是涉及到平均量混合概念,既然是直接提到平均速度,构建模型利用十指交叉法即可算出。假设山路长为12,则小王上山的时间为12/4=3,下山时间为12/6=2。
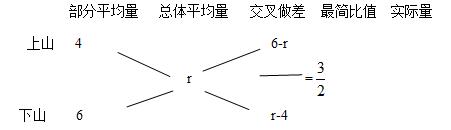
求解6-4=2按照3+2来分,每份0.4,3份对应1.2,则r=4.8。选A。
例3.某高校2006度毕业学生7650名,比上年度增长2%,其中本科生毕业数量比上年度减少2%,而研究生毕业数量比上年度增加10%,那么,这所高校今年毕业的本科生有()。
A.3920人 B.4410人 C.4900人 D.5490人
【解析】资料分析中,增长率=增长量/上一年的量,增长率也相当于平均量,也可看成混合问题,同样可利用十字交叉法,分别列出五部分所对应的值。

最简比,分母实际表示的量为上一年的本科生人数和研究生人数,因此交叉作差后的比应该为2005年的本科生与研究生之比,即2:1,也即2005年一共的人数为3份,而2005年总的人数=7650/(1+50%)=7500,即是一份所对应的是2500人,2005年本科生占2份,所以共5000人,则今年本科生有5000×(1-2%)=4900人。
综上发现,实际在涉及平均量混合问题时可以巧妙利用十字交叉法去解题。尤其是浓度混合问题、利润混合问题等在利用十字交叉方法解题时一定要注意,十字交叉后得到的比为求部分平均量分母的比,例如:利润的混合问题要注意是否为同种商品或者是成本之比,如果是不同种商品,那么成本之比就不是商品个数之比,要因题而异,切记生搬硬套公式。
![]() 注:本站稿件未经许可不得转载,转载请保留出处及原文地址。
注:本站稿件未经许可不得转载,转载请保留出处及原文地址。

扫描左侧二维码或者手动搜索cqwzks666,关注【重庆文职考试】,及时掌握军队文职考试资讯。
| 省份 | * |
|---|---|
| 姓名 | * |
| 电话 | * |
| 微信 | |