
在数量关系中大家肯定遇到过这样一类题目,我们知道几个数的加和,然后然让你去求其中某个数的最大值或者最小值,其实这一类题目就是和定最值问题。当碰到这一类问题时很多同学都会感到头疼,那么到底怎样解决这种题目呢,今天我们就来探讨一下。
比如我们来看这样一道题目:有21棵树要种在大小不同的5个区域,根据区域大小不同,所种数量各不相同,且每个区域都有树,问种树最多的区域最多有几棵?
我们首先来分析一下,有5个不同区域种树,那我们就画出五个位置,题目中要求最多的区域最多有多少,在树木总数一定的情况下,如过想让最多的区域尽量多,那么其他位置就应该尽量少,最少的区域最少能有1棵,又因为互不相同,第二少的区域最少有2棵,以此类推,得到最多的区域有21-1-2-3-4=11棵。分析过程如图1所示:
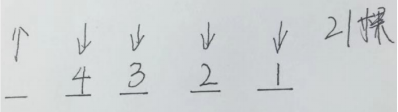
图1
接下来我们再来看下一道题:有21棵树要种在大小不同的5个区域,根据区域大小不同,所种数量各不相同,且每个区域都有树,问种树最多的区域最少有几棵?
和上面的题目相比较,我们发现上一个题是求最大数的最大值,此题是求最大区域最少种几棵,同样我们先画出5个位置,我们来分一下,要保证最多的区域所种数量尽可能少,在和一定的情况下,其他位置应该尽可能多,但第二多的区域再多也应该比最多的区域少,又因为每个区域各不相同,那么第二大的区域应该比最多的区域少一棵。以此类推,每一个区域都应该比前面的区域少一颗,所以5个区域数量构成了公差为1的等差数列。我们知道,等差数列的中项也是数列的平均,可以求得五个数平均数为21÷5=4…1,也就是说第三多的区域有4棵,那么最多的区域最少有6棵,但是还有一棵没分配,只能放在最多的区域,因此最多的区域最少有7棵。分析过程如图2所示:
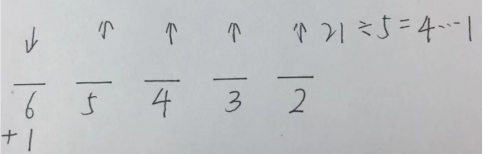
图2
根据上面的两道题目,其实我们可以总结一下和定最值的解题思路:
1、画图(画出分配位置,位置过多时可画出标志性位置)
2、分析标数(依据题目要求,运用逆向思维进行分析标数)
3、构造数列(依据各数据关系及等差数列中项求和公式将各位置用等差数列表示)
4、将余数补齐(根据题目要求将余数合理分配到相应位置)
![]() 注:本站稿件未经许可不得转载,转载请保留出处及原文地址。
注:本站稿件未经许可不得转载,转载请保留出处及原文地址。

扫描左侧二维码或者手动搜索cqwzks666,关注【重庆文职考试】,及时掌握军队文职考试资讯。
| 省份 | * |
|---|---|
| 姓名 | * |
| 电话 | * |
| 微信 | |